What is the “The Average House Price”?…
Some interesting thoughts
There are two different methods of calculating the average price in use at the moment – the Arithmetic mean and the Geometric Mean.
For August 2019 the ONS House Price Index reported that the average house price in England & Wales (seasonally adjusted) was £242,103. This compared to Acadata’s (seasonally adjusted) average house price for August 2019 for England & Wales of £298,934 – a 19% difference.
The main reason that the ONS average house price differed from our own is that the ONS calculates its averages using a “geometric mean” whereas we (along with others) use an “arithmetic mean”.
Let us look at some examples to show how the difference arises. If anyone wishes to follow these calculations in Excel the respective functions are =AVERAGE(House 1, House 2, House 3, House 4, House 5) for the Arithmetic Mean and =GEOMEAN(House 1, House 2, House 3, House 4, House 5) for the Geometric Mean.
A sample street with 5 houses (Scenario One):-
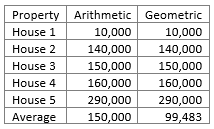
The Arithmetic Mean is £150,000 and the Geometric Mean is 99,483 – a 33% difference. A slightly contrived street perhaps – but it will highlight the main differences.
Let us now increase every house price by 10% (Scenario Two):-
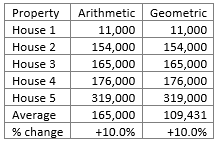
The Arithmetic and Geometric means both increase by 10% – so far so good
Let us now put all prices back to Scenario One levels except for House 3 , where we will say the increase is 10% (Scenario Three):-
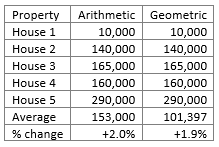
The Arithmetic mean increases by 2.0% while the Geometric mean increases by 1.9%.
Let us now put all prices back to Scenario One levels except for House 5 – the really expensive house – where we will say the increase is 10% (Scenario Four):-
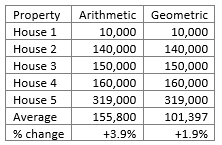
The Arithmetic Mean has increased by +3.9% but the increase in the Geometric Mean remains the same as Scenario Three at +1.9%. Incidentally the total spend if we purchased all five houses in Scenario Four would be £779,000 – a 3.9% increase in total spend over Scenario One’s total spend of £750,000.
Finally let us put all prices back to Scenario One levels except for House 1 – the low value house – where we will say the increase is 10% (Scenario Five):-
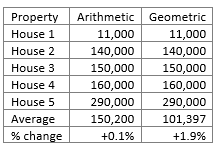
The Arithmetic Mean has only increased by +0.1% but the increase in the Geometric Mean remains the same as Scenario Three and Scenario Four at +1.9%. The total spend if we purchased all five houses in Scenario Five would be £751,000 – a 0.1% increase in total spend over Scenario One’s total spend of £750,000.
So there we have it – the Geometric mean will produce a constant growth rate relating to the % increase in the value of a home – irrespective of the value of that home – whereas the arithmetic mean will be dependent on the total expenditure that takes place in the market.
Now whether you consider the £1,000 increase in price under Scenario One should be the equivalent of the £29,000 increase in price under Scenario Four is another matter.
